翻译

计算小于一个非负整数n的质数的个数。

原文

Count the number of prime numbers less than a non-negative number, n.

分析

这道题以前遇到过，当时是用的最笨的办法，现在也没什么好想法，又恰好题目有提示，我就点开了。题目的提示是一条一条给出来的，我也就逐个的全点开了，感觉好失败……

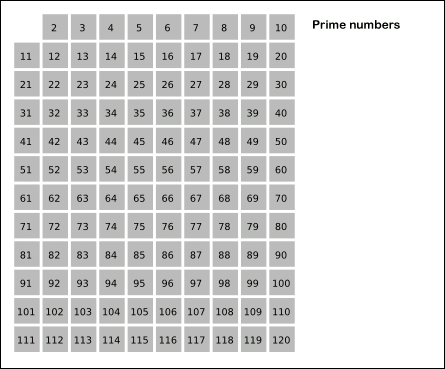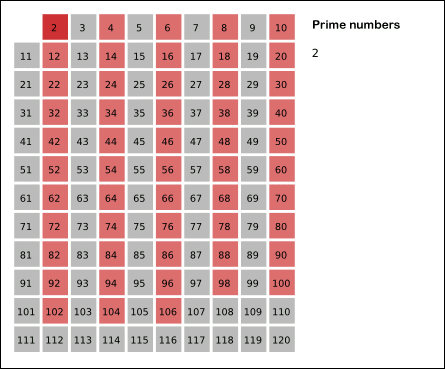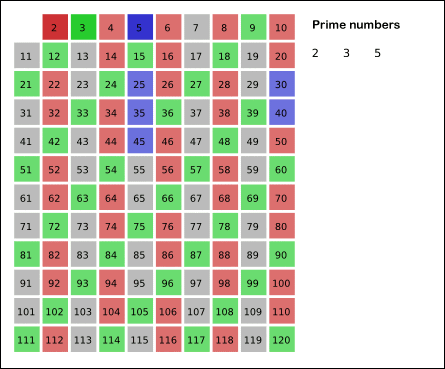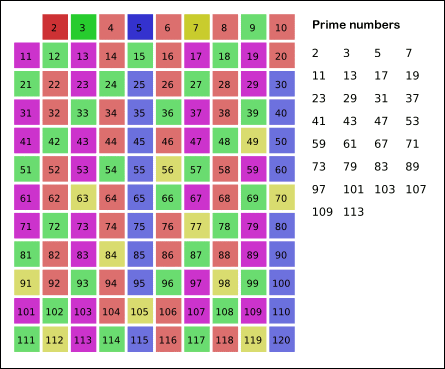
public int countPrimes(int n) {   int count = 0;   for (int i = 1; i < n; i++) {      if (isPrime(i)) count++;   }   return count;}private boolean isPrime(int num) {   if (num <= 1) return false;   // Loop's ending condition is i * i <= num instead of i <= sqrt(num)   // to avoid repeatedly calling an expensive function sqrt().   for (int i = 2; i * i <= num; i++) {      if (num % i == 0) return false;   }   return true;}

The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. I promise that the concept is surprisingly simple.

public int countPrimes(int n) {   boolean[] isPrime = new boolean[n];   for (int i = 2; i < n; i++) {      isPrime[i] = true;   }   // Loop's ending condition is i * i < n instead of i < sqrt(n)   // to avoid repeatedly calling an expensive function sqrt().   for (int i = 2; i * i < n; i++) {      if (!isPrime[i]) continue;      for (int j = i * i; j < n; j += i) {         isPrime[j] = false;      }   }   int count = 0;   for (int i = 2; i < n; i++) {      if (isPrime[i]) count++;   }   return count;}

以上均为LeetCode原文……

把上面的代码翻译一下成如下：

class Solution {public:    bool isPrime(int num) {        if (num <= 1) return false;        for (int i = 2; i*i <= num; ++i) {            if (num%i == 0) return false;        }        return true;    }    int countPrimes(int n) {        bool *isPrime = new bool[n];        for (int i = 2; i < n; ++i) {            isPrime[i] = true;        }        for (int i = 2; i*i < n; ++i) {            if (!isPrime[i]) continue;            for (int j = i*i; j < n; j += i) {                isPrime[j] = false;            }        }        int count = 0;        for (int i = 2; i < n; ++i) {            if (isPrime[i]) count++;        }        return count;    }};

摘录一些代码：

class Solution {public:    int countPrimes(int n) {        switch(n) {            case 0:            case 1:            case 2: return 0;            case 3: return 1;            case 4:            case 5: return 2;            case 6:             case 7: return 3;            case 8:            case 9:             case 10:             case 11: return 4;            case 12:             case 13: return 5;            case 14:             case 15: return 6;            case 10000: return 1229;            case 499979: return 41537;            case 999983: return 78497;            case 1500000: return 114155;        }    }};

int countPrimes(int n) {    if(--n < 2) return 0;    int m = (n + 1)/2, count = m, k, u = (sqrt(n) - 1)/2;    bool notPrime[m] = {
    0};    for(int i = 1; i <= u;i++)        if(!notPrime[i])          for(k = (i+ 1)*2*i; k < m;k += i*2 + 1)              if (!notPrime[k])              {                  notPrime[k] = true;                  count--;              }    return count;}